Advertisements
Advertisements
प्रश्न
Find the area of each of the following figure:
उत्तर
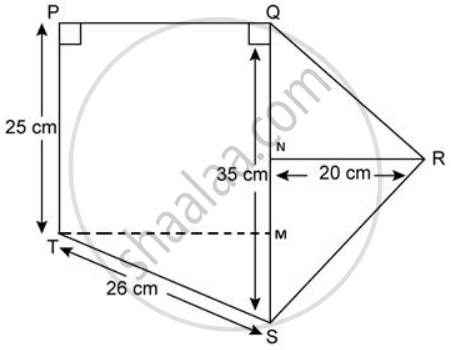
Construction: Draw TM ⊥ QS
Area of ΔRQS
= `(1)/(2) xx "QS" xx "RN"`
= `(1)/(2) xx 35 xx 20`
= 350cm2
Now,
S = QM + MS
⇒ 35 = 25 + MS
⇒ MS = 10cm
In ΔSTM,
MS2 + TM2 = ST2
⇒ TM2 = ST2 - MS2
= (26)2 - (10)2
= 676 - 100
= 576
⇒ TM
= 24cm
= PQ
Area of trapezium PQST
= `(1)/(2) xx ("PT" + "QS") xx "PQ"`
= `(1)/(2) xx (25 + 35) xx 24`
= 720cm2
Thus, area of given figure
= Area of ΔRQS + Area of trapezium PQST
=350cm2 + 720cm2
= 1070cm2.
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a square are equal and bisect each other at right angles.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.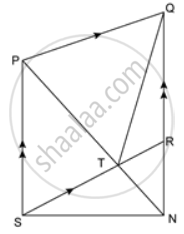
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
In the given figure, ABC is a triangle and AD is the median.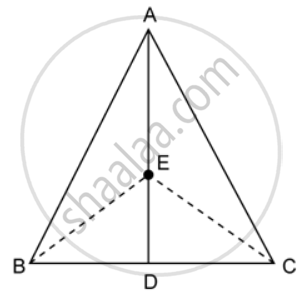
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
In the given figure, ABC is a triangle and AD is the median.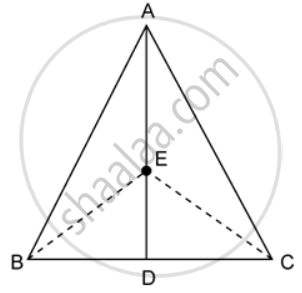
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
The diagonals of a square are perpendicular to one another.
All the sides of a rhombus are of equal length.
The opposite sides of a trapezium are parallel.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

