Advertisements
Advertisements
Question
Find the area of each of the following figure: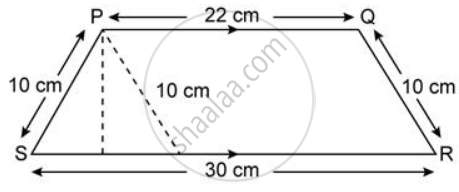
Solution
Clearly opposite sides of quadrilateral PQRT are parallel, it is a parallelogram.
ST
= SR - TR
= 30 - 22
= 8cm
In ΔPST,
Let a = PS = 10cm, b = ST = 8cm and C = TP = 10cm
∴ s = `("a" + "b" + "c")/(2)`
= `(10 + 8 + 10)/(2)`
= `(28)/(2)`
= 14cm
Area of ΔPSR
= `sqrt("s"("s"- "a")("s" - "b")("s"-"c")`
= `sqrt(14(14 - 10)(14 - 8)(14 - 10)`
= `sqrt(14 xx 4 xx 6 xx 4)`
= `8sqrt(21)"cm"^2`
If PM is taken height corresponding to base ST,
Area of ΔPST
= `(1)/(2) xx "ST" xx "PM"`
⇒ `8sqrt(21) = (1)/(2) xx 8 xx "PM"`
⇒ PM = `2sqrt(21)"cm"`
∴ Area of given figure
= `(1)/(2) xx("PQ" + "SR") xx "PM"`
= `(1)/(2) xx (22 + 30) xx 2sqrt(21)`
= `(1)/(2) xx 52 xx 2sqrt(21)`
= `52sqrt(21)"cm"^2`.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.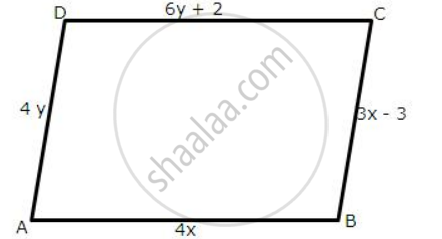
find the values of x and y.
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.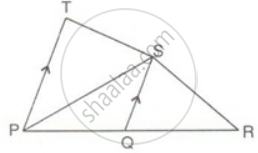
Prove that the median of a triangle divides it into two triangles of equal area.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
In the given figure, ABC is a triangle and AD is the median.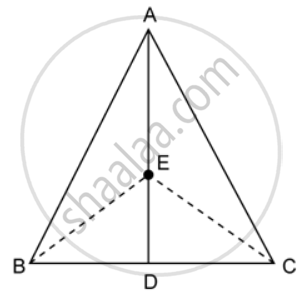
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.
Make two more examples of this.
Name polygon.

Make two more examples of this.
