Advertisements
Advertisements
प्रश्न
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
उत्तर
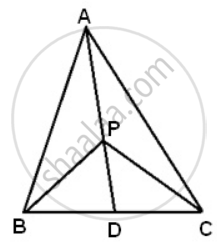
AD is the median of ΔABC, so, it will divide ΔABC into two triangles of equal areas.
Therefore, Area(ΔABD) = area(ΔACD) ...(1)
Now PD is the median of ΔPBC.
Therefore, Area(ΔPBD) = area(ΔPCD) ...(2)
Subtract equation (2) from equation (1), we have
Area(ΔABD) - area(ΔPBD) = Area(ΔACD) - Area(ΔPCD)
Area(ΔABP) = area(ΔACP).
APPEARS IN
संबंधित प्रश्न
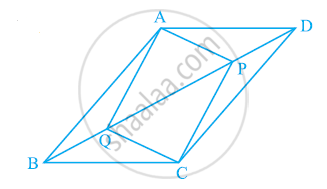
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.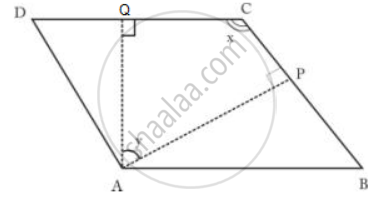
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.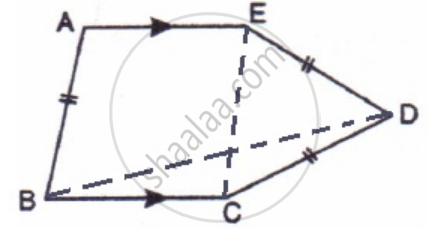
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.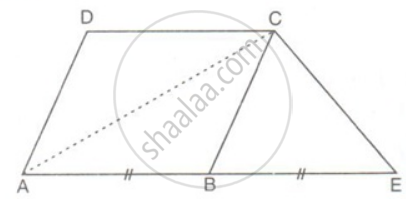
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure: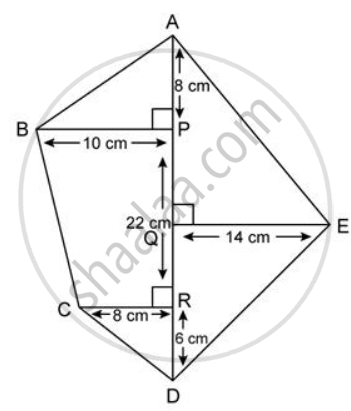
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
The diagonals of a square are perpendicular to one another.
Give reason for the following :
A square can be thought of as a special rectangle.
Name polygon.
Make two more examples of this.
Name polygon.

Make two more examples of this.
