Advertisements
Advertisements
प्रश्न
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
उत्तर
The perimeter of a square with side s = p = 4s
∴ Here, the perimeter of the square are 128cm and 96cm
∴ the sides of the two squares are 32cm and 24cm
We know, The area of a square with side s = s2
∴ the areas of the two squares are = 32cm2 = 1024cm2 and 24cm2 = 576cm2
∴ the combined area
= area of the new square
= 1024cm2 + 576cm2
= 1600cm2
the side of the square
= `sqrt(1600)`
= 40cm
The perimeter of a square with side 40
= 4 x 40
= 160cm
The sides and diagonal of a square from a right triangle as each angle of a square is a right angle.
Diagonal is the side opposite to the right angle, therefore it is the hypotenuse
Here, diagonal of the square
= `sqrt(40^2 + 40^2)`
= `40sqrt(2)`
= 40(1.414)
= 56.57cm.
APPEARS IN
संबंधित प्रश्न
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.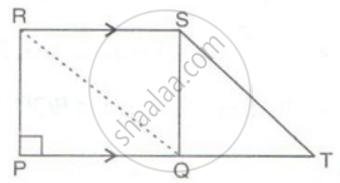
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.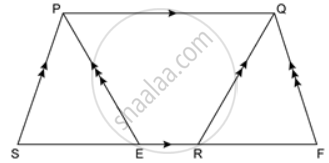
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.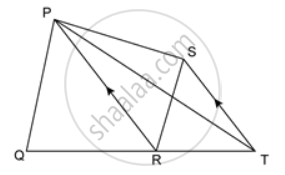
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.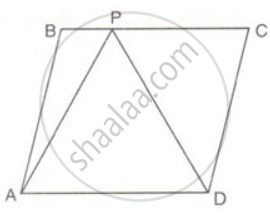
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure:
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Each angle of a rectangle is a right angle.
