Advertisements
Advertisements
प्रश्न
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
उत्तर
Let the sides of the rectangular field = 8x and 5x
So, the sides of the rectangular field after leaving the path of 2m on all sides = 8x - 4 and 5x - 4
Area of the rectangular field = (8x) (5x)
Area of the rectangular field after leaving the path of 2m on all sides = (8x - 4)(5x - 4)
Area of the path of 2m on all sides
= (8x)(5x) - (8x - 4)(5x - 4)
= 40x2 - (40x2 - 32x - 20x + 16)
= 848
52x + 16 = 848
x = 16
The sides of the rectangular field
= 8x and 5x
= 128m and 80m.
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.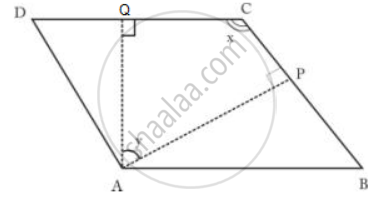
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.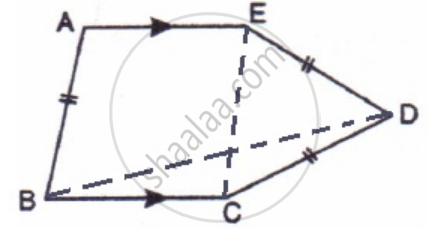
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.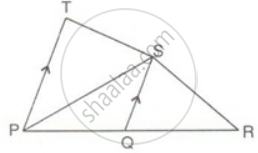
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.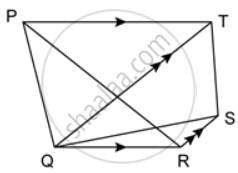
*Question modified
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
In the given figure, ABC is a triangle and AD is the median.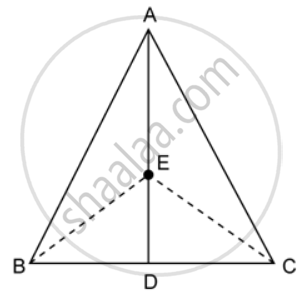
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of each of the following figure:
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
