Advertisements
Advertisements
प्रश्न
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.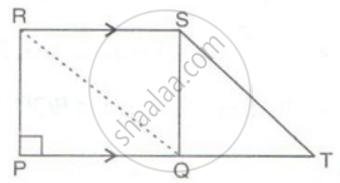
उत्तर
(i) ar(ΔQTS) = `(1)/(2)` x ar(parallelogram QTSR)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
⇒ ar(parallelogram QTSR) = 2 x ar(ΔQTS)
⇒ ar(parallelogram QTSR) = 2 x 60cm2
⇒ ar(parallelogram QTSR) = 120cm2
(ii) ar(ΔQTS) = `(1)/(2)` x ar(parallelogram QTSR)
ar(ΔQTS) = ar(ΔRSQ) = 60cm2
Now,
ar(ΔRSQ) = `(1)/(2)` x ar(rectangle PQRS)
⇒ ar(rectangle PQRS) = 2 x ar(ΔRSQ)
⇒ ar(rectangle PQRS) = 2 x 60cm2
⇒ ar(rectangle PQRS) = 120cm2
(iii) Since PQRS is a rectangle,
Therefore RS = PQ .....(i)
QTSR is a parallelogram,
Therefore, RS = QT .....(ii)
From (i) and (ii)
PQ = QT .......(iii)
In ΔPSQ and ΔQST
QS = QS
PQ = QT ...(from (iii))
∠PQS = ∠SQT = 90°
Therefore, ΔPSQ ≅ ΔQST
Area of two congruent triangles is equal.
Hence, ar(ΔPSQ) = ar(ΔQTS) = 60cm2.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
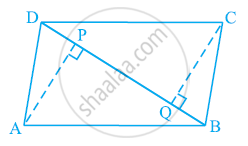
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
In the given figure, ABC is a triangle and AD is the median.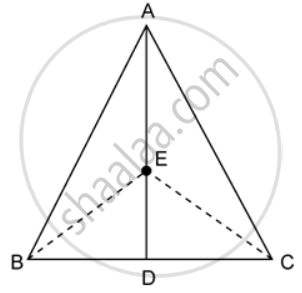
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
The diagonals of a square are perpendicular to one another.
All the sides of a rhombus are of equal length.
The opposite sides of a trapezium are parallel.
Give reasons for the following :
A square can be thought of as a special rhombus.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
