Advertisements
Advertisements
प्रश्न
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
उत्तर
Let the side of the smaller square = x
∴ the side of the larger square = x + 4
We know, The area of a square with side s = s2
∴ The area of a square with side x = x2
and, The area of a square with side x + 4 = (x + 4)2
Now, the sum of the two area = 400
⇒ x2 + (x+ 4)2 = 400
⇒ x2 + x2 + 16 + 8x = 400
⇒ 2x2 + 8x + 16 = 400
⇒ 2(x2 + 4x + 8) = 2(200)
⇒ x2 + 4x + 8 = 200
⇒ x2 + 4x - 192 = 0
Splittting the middle term, we have
x2 + 16x - 12x - 192 = 0
⇒ x(x + 16) - 12(x + 16) = 0
⇒ (x + 16)(x - 12) = 0
⇒ x = -16, x = 12
But x is the length of the side of a square,
∴ x ≠ -16
∴ x = 12
⇒ the side ofthe smaller square = 12cm
∴ the side of the larger square
= 12 + 4
= 16cm.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
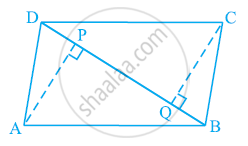
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.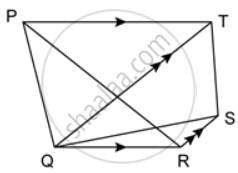
*Question modified
In the given figure, ABC is a triangle and AD is the median.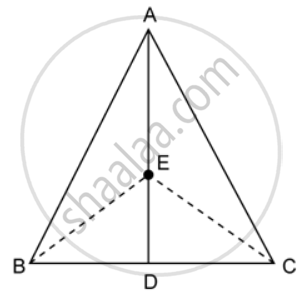
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
The opposite sides of a rectangle are equal in length.
All the sides of a rhombus are of equal length.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Give reason for the following :
Square is also a parallelogram.
Examine whether the following is a polygon. If it is not, say why?

