Advertisements
Advertisements
प्रश्न
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.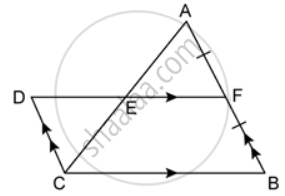
उत्तर
In ΔABC,
AF = FB and EF || BC ...(given)
∴ AE = EC ...(Converse of Midpoint theorem) ...(i)
In ΔAEF and ΔCED,
∠FEA = ∠DEC ...(Vertically opposite angles)
CE = AE ...[From (i)]
∠FAE = ∠DCE ...(Alternate angles)
∴ ΔFAE ≅ ΔCED ...( ASA test of congruency)
⇒ A(ΔAEF) = A(ΔCED) ....(ii)
A(ΔABC)
= A(ΔAEF) + A(EFBC)
= A(ΔCED) + A(EFBC) ....[From (ii)]
∴ A(ΔABC) = A(||gm DCBF)
⇒ A(||gm DCBF) = 30 sq. units.
APPEARS IN
संबंधित प्रश्न
All rectangles are squares
All squares are not parallelograms.
Identify all the quadrilaterals that have four right angles
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
Prove that the bisectors of the interior angles of a rectangle form a square.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;
prove that AP and DQ are perpendicular to each other.
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.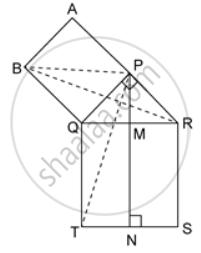
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
