Advertisements
Advertisements
प्रश्न
Prove that the median of a triangle divides it into two triangles of equal area.
उत्तर
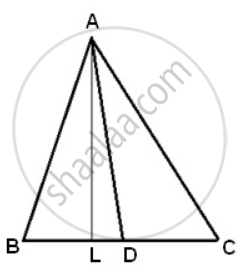
Draw AL perpendicular to BC.
Since AD is median of ΔABC. Therefore, D is the mid-point of BC.
⇒ BD = DC
⇒ BD x AL = DC x AL ...(multiplying by AL)
⇒ `(1)/(2)("BD" xx "AL")`
= `(1)/(2)("DC" xx "AL")`
⇒ ar(ΔABD) = ar(ΔADC).
APPEARS IN
संबंधित प्रश्न
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.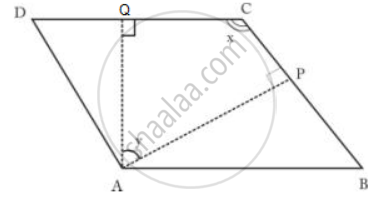
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.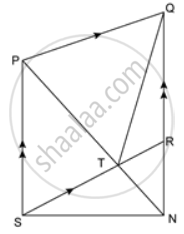
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.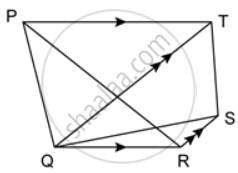
*Question modified
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
In the given figure, ABC is a triangle and AD is the median.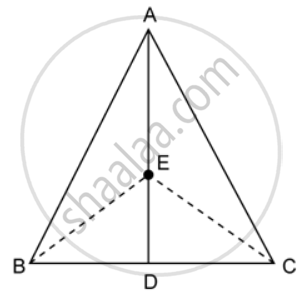
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of each of the following figure: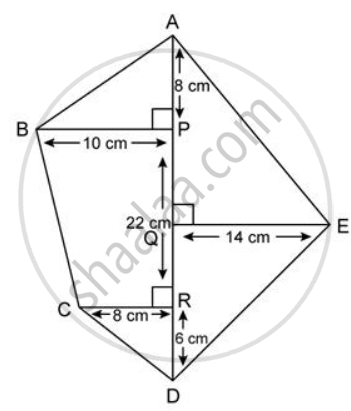
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
The opposite sides of a rectangle are equal in length.
Name polygon.

Make two more examples of this.
