Advertisements
Advertisements
प्रश्न
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.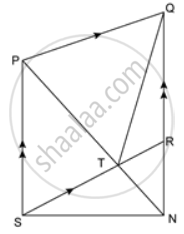
उत्तर
ΔPQT and parallelogram PQRS are on the same base PQ and between the same parallel lines PQ and SR.
∴ Δ(ΔPQT) = `(1)/(2)"A"`(parallelogram PQRS) ....(i)
ΔPSN and parallelogram PQRS are on the same base PS and between the same parallel lines PS and QN.
∴ Δ(ΔPSN) = `(1)/(2)"A"`(parallelogram PQRS) ....(ii)
Adding equations (i) and (ii), we get
∴ A(ΔPQT) + A(ΔPSN) = A(parallelogram PQRS)
⇒ A(quad. PSNQ) - A(ΔQTN) = A(parallelogram PQRS)
⇒ A(quad. PSNQ) - A(ΔQTN) = A(quad. PSNQ) - A(ΔSRN)
⇒ A(ΔQTN = A(ΔSRN)
Subtracting A(ΔRTN) from both the sides, we get
A(ΔQTN) - A(ΔRTN) = A(ΔSRn) - A(ΔRTN)
⇒ A(ΔQTR) = A(ΔSTN).
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
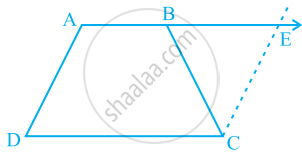
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.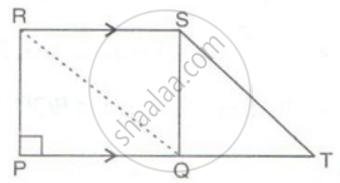
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.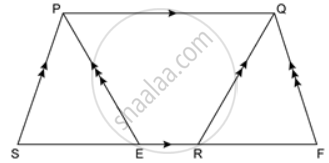
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.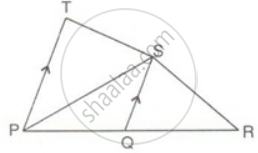
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.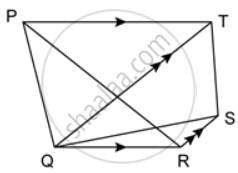
*Question modified
Find the area of each of the following figure:
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
All the sides of a parallelogram are of equal length.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Give reasons for the following :
A square can be thought of as a special rhombus.
Name polygon.
Make two more examples of this.
