Advertisements
Advertisements
प्रश्न
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

उत्तर
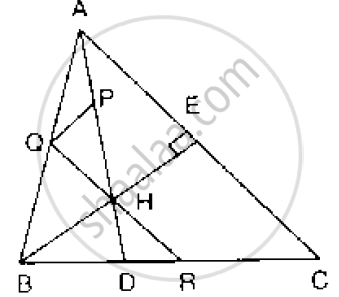
Given
BE ⊥ AC and P, Q and R are respectively midpoint of AH , AB and BC
To prove:
`∠`PQRD = 90°
Proof: In ΔABC, Q and R are midpoints of AB and BC respectively
∴QR || AC ......(i )
In ΔABH , Q and P are the midpoints of AB and AH respectively
∴ QP || BH
⇒ QP || BE ......(ii )
But, AC ^ BE ∴ from equation (i) and equation (ii) we have
QP ⊥ QR
⇒ `∠`PQR = 90°, hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

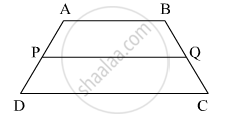
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 4CR = AB.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
