Advertisements
Advertisements
Question
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
Solution
Given: In quadrilateral ABCD, P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
Also, AC = BD and AC ⊥ BD.
To prove: PQRS is a square.
Proof: Now, in ΔADC, S and R are the mid-points of the sides AD and DC respectively, then by mid-point theorem,
SR || AC and SR = `1/2` AC ...(i)
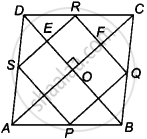
In ΔABC, P and Q are the mid-points of AB and BC, then by mid-point theorem,
PQ || AC and PQ = `1/2` AC ...(ii)
From equations (i) and (ii),
PQ || SR and PQ = SR = `1/2` AC ...(iii)
Similarly, in ΔABD, by mid-point theorem,
SP || BD and SP = `1/2` BD = `1/2` AC [Given, AC = BD] ...(iv)
And ΔBCD, by mid-point theorem,
RQ || BD and RQ = `1/2` BD = `1/2` AC [Given, BD = AC] ...(v)
From equations (iv) and (v),
SP = RQ = `1/2` AC ...(vi)
From equations (iii) and (vi),
PQ = SR = SP = RQ
Thus, all four sides are equal.
Now, in quadrilateral OERF,
OE || FR and OF || ER
∴ ∠EOF = ∠ERF = 90° ...[∵ AC ⊥ DB ⇒ ∠DOC = ∠EOF = 90° as opposite angles of a parallelogram]
∴ ∠QRS = 90°
Similarly, ∠RQS = 90°
So, PQRS is a square.
Hence proved.
APPEARS IN
RELATED QUESTIONS
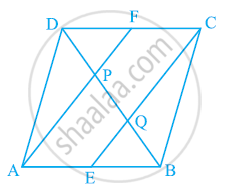
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
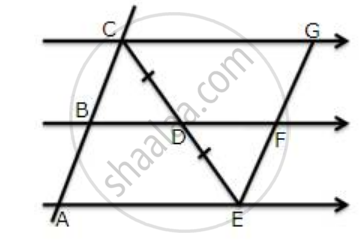
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
