Advertisements
Advertisements
Question
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 4CR = AB.
Solution
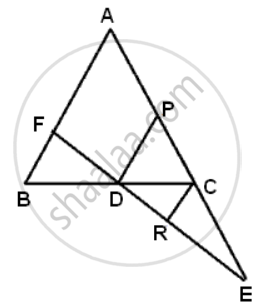
In ΔDEP,
C and R are the mid-points of PE and DE respectively.
Also, DP || RC
∴ CR = `(1)/(2)"DP"`......(i)
In ΔABC,
D and P are the mid-points of BC andAC respectively.
Also, DP || AB
∴ DP = `(1)/(2)"AB"`......(ii)
Substituting the value of DP from (ii) and(i)
⇒ CR = `(1)/(2)(1/2 "AB")`
⇒ CR = `(1)/(4)"AB"`
∴ 4CR = AB.
APPEARS IN
RELATED QUESTIONS
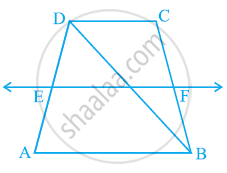
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
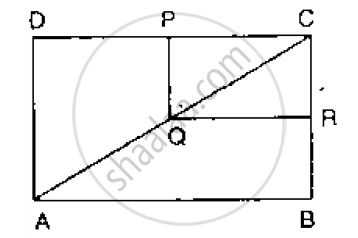
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
