Advertisements
Advertisements
Question
ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.
Solution
Given: ABCD is a quadrilateral such that AB || DC and AD = BC
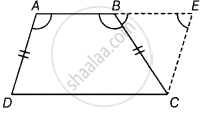
Construction: Extend AB to E and draw a line CE parallel to AD.
Proof: Since, AD || CE and transversal AE cuts them at A and E, respectively.
∴ ∠A + ∠E = 180° ....[Since, sum of cointerior angles is 180°]
⇒ ∠A = 180° – ∠E ...(i)
Since, AB || CD and AD || CE
So, quadrilateral AECD is a parallelogram.
⇒ AD = CE
⇒ BC = CE ...[∵ AD = BC, given]
Now, in ΔBCE
CE = BC ...[Proved above]
⇒ ∠CBE = ∠CEB ...[Opposite angles of equal side are equal]
⇒ 180° – ∠B = ∠E ...[∵ ∠B + ∠CBE = 180°]
⇒ 180° – ∠E = ∠B ...(ii)
From equations (i) and (ii),
∠A = ∠B
Hence proved.
Notes
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A convex quadrilateral
Define the following term Convex Quadrilateral .
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite sides.
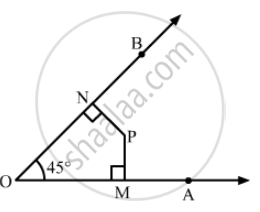
In Fig. 16.20, find the measure of ∠MPN.
Mark the correct alternative in each of the following:
The opposite sides of a quadrilateral have
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =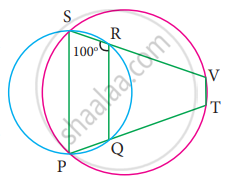
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
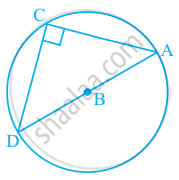
Using the information given, name the right angles in part of figure:
AC ⊥ CD