Advertisements
Advertisements
Question
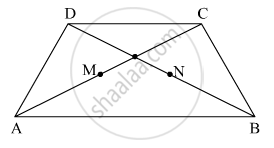
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
Solution
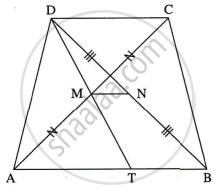
Given: `square`ABCD is a trapezium. AB || DC
Points M and N are the midpoints of diagonals AC and DB respectively.
To prove: MN || AB
Construction: Draw line DM which intersects side AB at point T.
Proof:
side DC || side AB …(Given)
And seg AC is a transversal line.
∴ ∠DAC ≅ ∠BAC ...(alternate angles)
∴ ∠DCM ≅ ∠TAM ...(i) ...(A-M-C and A-T-B)
In ∆DCM and ∆TAM,
∠DCM ≅ ∠TAM ...[From (i)]
seg MC ≅ seg MA ...(Point M is the midpoint of seg AC.)
∠DCM ≅ ∠TAM ...(Vertically opposite angles)
∴ ∆DCM ≅ ∆TAM ...(ASA test)
seg DM ≅ seg MT ...(c.s.c.t) ...(ii)
In ∆DTB,
Point N is the midpoint of line DB. ...(Given)
Point M is the midpoint of line DT. ...[From (ii)]
∴ seg MN || side TB ...(Midpoint Theorem)
∴ seg MN || seg AB ...(A-T-B)
APPEARS IN
RELATED QUESTIONS
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
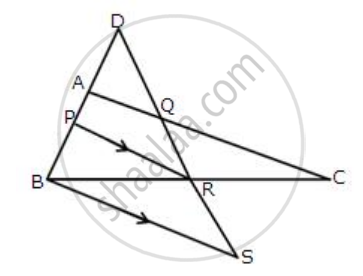
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.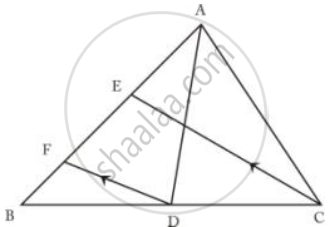
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
