Advertisements
Advertisements
Question
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
Solution
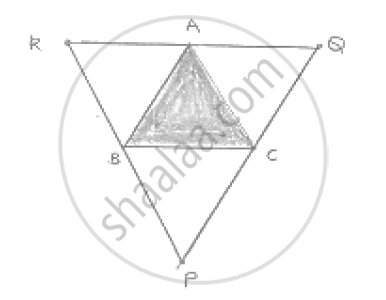
Clearly ABCQ and ARBC are parallelograms.
∴ BC = AQ and BC = AR
⇒ AQ = AR
⇒ A is the midpoint of QR .
Similarly B and C are the midpoints of PR and PQ respectively
∴ AB = `1/2` PQ, BC = `1/2` QR, CA = `1/2 `PR
⇒ PQ = 2AB,QR = 2BC and PR = 2CA
⇒ PQ + QR + RP = 2( AB + BC + CA)
⇒ Perimeter of DPQR = 2 [Perimeter of DABC ]
APPEARS IN
RELATED QUESTIONS
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
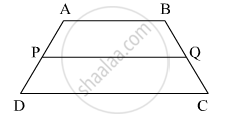
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm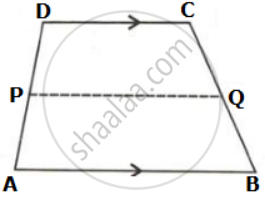
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
