Advertisements
Advertisements
Question
Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ∆ABC as shown in the following figure. Show that BC = `1/2` QR.
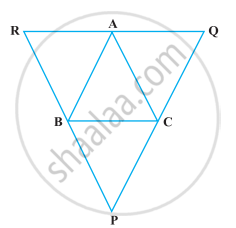
Solution
Given In ΔABC, PQ || AB and PR || AC and RQ || BC.
To show BC = `1/2` QR
Proof In quadrilateral BCAR, BR || CA and BC || RA
So, quadrilateral, BCAR is a parallelogram.
BC = AR ...(i)
Now, in quadrilateral BCQA,
BC || AQ
And AB || QC
So, quadrilateral BCQA is a parallelogram,
BC = AQ ...(ii)
On adding equations (i) and (ii), we get
2BC = AR + AQ
⇒ 2BC = RQ
⇒ BC = `1/2` QR
Now, BEDF is a quadrilateral, in which ∠BED = ∠BFD = 90°
∠FSE = 360° – (∠FDE + ∠BED + ∠BFD)
= 360° – (60° + 90° + 90°)
= 360° – 240°
= 120°
APPEARS IN
RELATED QUESTIONS
`square`ABCD is a parallelogram, P and Q are midpoints of side AB and DC respectively, then prove `square`APCQ is a parallelogram.

ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.
