Advertisements
Advertisements
Question
The measure of angles of a hexagon are x°, (x − 5)°, (x − 5)°, (2x − 5)°, (2x − 5)°, (2x + 20)°. Find the value of x.
Solution
\[\text{ Since the sum of all the angles of a hexagon is } 720° , \text{ we get } : \]
\[x° + \left( x - 5 \right)° + \left( x - 5 \right)° + \left( 2x - 5 \right)° + \left( 2x - 5 \right)° + \left( 2x + 20 \right)° = 720°\]
\[ \Rightarrow x° + x° - 5° + x°- 5°+ 2x - 5°+ 2x - 5°+ 2x + 20°= 720° \]
\[ \Rightarrow 9x - 20° + 20° = 720° \]
\[ \Rightarrow 9x = 720° \]
\[ \therefore x = 80\]
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A convex quadrilateral
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite angles are there?
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
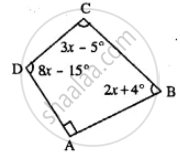
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = x° and ∠D = (3x – 20)°; find the value of x.
In an isosceles trapezium one pair of opposite sides are _____ to each Other and the other pair of opposite sides are _____ to each other.
Angle A of an isosceles trapezium ABCD is 115°; find the angles B, C and D.
Calculate the measure of each angle of a nonagon.
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite angles.
