Advertisements
Advertisements
Question
Angle A of an isosceles trapezium ABCD is 115°; find the angles B, C and D.
Solution
Since the base angles of an isosceles trapezium are equal,
∴ ∠A = ∠B = 115°
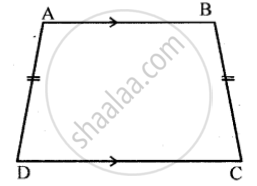
Also, ∠A and ∠D are co-interior angles and their sum = 180°
∴ ∠A + ∠D = 180°
⇒115° + ∠D = 180°
⇒ ∠D = 180° - 115°
⇒ ∠D = 65°
Also, ∠D = ∠C = 65°
∴ ∠B = 115°, ∠C = 65°, ∠D = 65°
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Opposite sides .
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent angles are there?
A quadrilateral has all its four angles of the same measure. What is the measure of each?
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
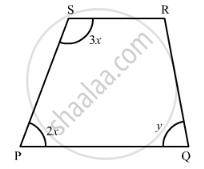
In the given figure, PQRS is an isosceles trapezium. Find x and y.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
Write two conditions that will make the adjoining figure a square.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =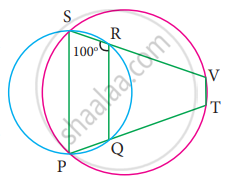
In quadrilateral WXYZ, the pairs of opposite angles are ______.
In given figure, name any four angles that appear to be acute angles.
Using the information given, name the right angles in part of figure:
AC ⊥ BD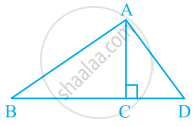
Using the information given, name the right angles in part of figure:
AE ⊥ CE
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?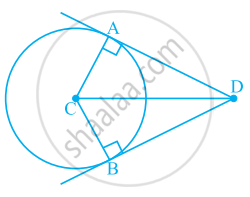
Can we have two obtuse angles whose sum is an acute angle? Why or why not?
Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite sides.
