Advertisements
Advertisements
Question
A quadrilateral has all its four angles of the same measure. What is the measure of each?
Solution
\[\text{ Let x be the measure of each angle } . \]
\[ \text{ Since, the sum of all the angles of a quadrilateral is } 360°, \text{ we have } : \]
\[x° + x° + x° + x° = 360°\]
\[ \Rightarrow 4x° = 360° \]
\[ \Rightarrow x°= 90° \]
\[ \therefore \text{ The measure of each angle is } 90° .\]
APPEARS IN
RELATED QUESTIONS
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
Define the following term Quadrilateral .
In a quadrilateral, define of the following Opposite sides .
Complete of the following, so as to make a true statement:
The number of pairs of adjacent angles of a quadrilateral is .......
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
In quadrilateral WXYZ, the pairs of opposite angles are ______.
In the given figure.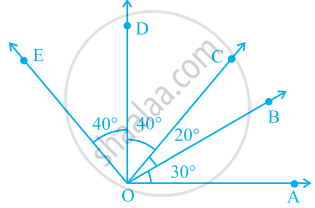
∠AOE is a/an ______ angle
In given figure, name any two angles that appear to be obtuse angles.
Using the information given, name the right angles in part of figure:
AE ⊥ CE
