Advertisements
Advertisements
Question
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is ______.
Options
55º
50º
40º
25º
Solution
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is 50º.
Explanation:
Let ABCD be a rectangle, where ∠CAB = 25°.
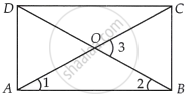
We know, diagonals of a rectangle are equal in length.
∴ AC = BD
⇒ `1/2 AC = 1/2 BD` ...[Dividing both sides by 2]
⇒ OA = OB ...[Since, O is the mid-point of AC and BD]
⇒ ∠2 = ∠1 ...[Angles opposite to equal sides are equal]
⇒ ∠2 = 25°
Now, ∠3 = ∠1 + ∠2 ...[Exterior angle is equal to the sum of two opposite interior angles]
= 25° + 25°
= 50°
Hence, the acute angle between the diagonals is 50°.
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A regular hexagon
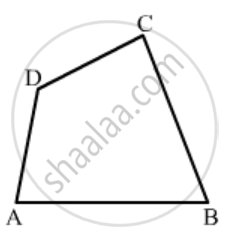
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite sides.
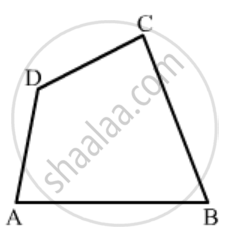
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent sides are there?
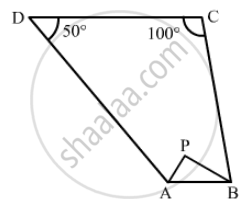
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
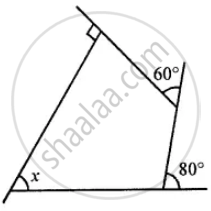
Use the following figure to find the value of x
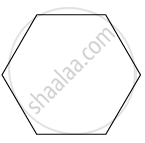
Observe the figure below and find out their name.
A quadrilateral can be drawn when all the four angles and one side is given.
Both the pairs of opposite angles of a quadrilateral are equal and supplementary. Find the measure of each angle.
Using the information given, name the right angles in part of figure:
AE ⊥ CE
