Advertisements
Advertisements
Question
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
Solution
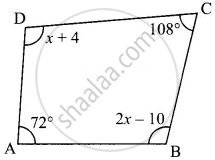
∠A = 72°
∠C = 180° – 12° ...(∠A and ∠C are supplementary)
= 108°
∠A + ∠B + ∠C + ∠D = 360° ...(Total angles of quadrilateral)
72° + 2x – 10 + 108° + x + 4 = 360°
3x + 174° = 360°
x = `(186^circ)/3`
= 62°
The value of x is 62°
∠B = 2x – 10
= 2(62°) – 10
= 124° – 10°
= 114°
∠D = x + 4
= 62° + 4
= 66°
The other angles are 114°, 62° and 66°.
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Diagonals .
A quadrilateral has three acute angles each measures 80°. What is the measure of the fourth angle?
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
Complete the following statement by means of one of those given in brackets against each:
If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a ...............
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?
Using the information given, name the right angles in part of figure:
BA ⊥BD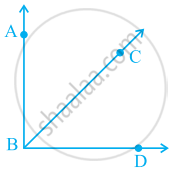
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?