Advertisements
Advertisements
Question
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
Solution
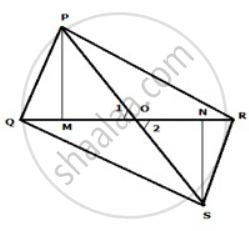
Join PS. Suppose PS and QR intersect at O. Draw PM and SN perpendicular to QR.
ar(ΔPQR) = ar(ΔSQR)
Thus ΔPQR and ΔSQR are on the same base QR and have equal area.
Therefore, their corresponding altitudes are equal i.e. PM = SN.
Now,
In ΔPMO and ΔSNO.
∠1 = ∠2 ...(vertically opposite angles)
∠PMO = ∠SNO ...(right angles)
PM = SN
Therefore, ΔPMO ≅ ΔSNO ..(AAS axiom)
⇒ PO = OS
⇒ QR bisects PS.
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
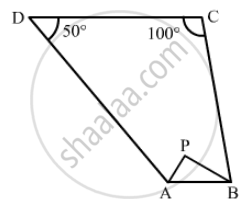
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
The consecutive sides of a quadrilateral have
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
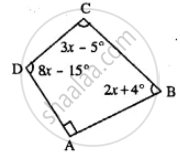
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
Calculate the measure of each angle of a nonagon.
In quadrilateral ROPE, the pairs of adjacent angles are ______.
In given figure, name any two angles that appear to be obtuse angles.
Using the information given, name the right angles in part of figure:
RS ⊥ RW
