Advertisements
Advertisements
प्रश्न
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
उत्तर
A pentagon has 5 sides
∴ Sum of interior angles
= (n - 2) x 180°
= (5 - 2) x 180°
= 3 x 180°
= 540°
Given, the angles are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°
∴ x °+ (x - 10)° + (x + 20)° + (2x - 44)° + (2x - 70)° = 540°
⇒ 7x° - 104° = 540°
⇒ x = `((540° + 104°))/(7)` = 92°
∴ The interior angles of the pentagon are 92°, 82°, 112°, 140° and 114°.
APPEARS IN
संबंधित प्रश्न
Define the following term Quadrilateral .
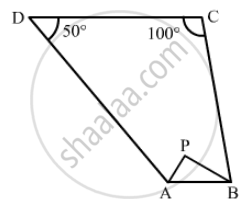
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is ______.
In the given figure.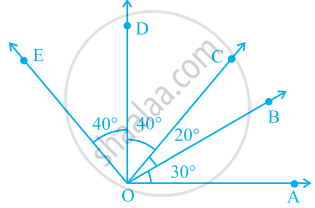
∠AOE is a/an ______ angle
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?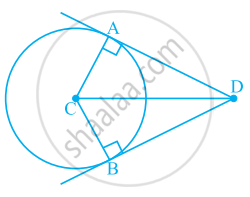
Can we have two obtuse angles whose sum is an acute angle? Why or why not?
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite sides.
