Advertisements
Advertisements
Question
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is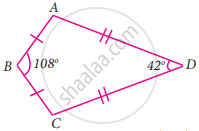
Options
150°
30°
105°
72°
Solution
105°
Explanation;
Hint:
Join BD
∠DBC = 54°; ∠BDC = 21°
∴ ∠BCD = 180° – (54° + 21°)
= 180° – 75°
= 105°
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Interior .
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite sides.
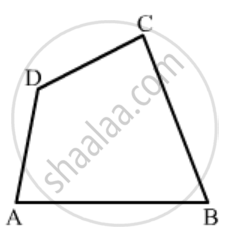
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
One diagonal of a rectangle is 18 cm. What is the length of its other diagonal?
In quadrilateral ROPE, the pairs of adjacent angles are ______.
Using the information given, name the right angles in part of figure:
AC ⊥ BD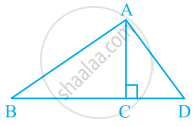
Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?