Advertisements
Advertisements
Question
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution
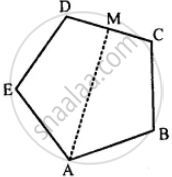
Given: ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove : ∠AMC = 90°
Proof: We know that the measure of each interior angle of a regular pentagon is 108°.
∠BAM = x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
54° + 108° + 108° + ∠AMC = 360°
∠AMC = 360° – 270°
∠AMC = 90°
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
A point is in the interior of a convex quadrilateral, if it is in the ..... of its two opposite angles.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite sides are there?
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite angles.

In the given figure, ABCD is a trapezium. Find the values of x and y.

In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
The angles A, B, C and D of a trapezium ABCD are in the ratio 3: 4: 5: 6. Le. ∠A : ∠B : ∠C : ∠D = 3:4: 5 : 6. Find all the angles of the trapezium. Also, name the two sides of this trapezium which are parallel to each other. Give reason for your answer.
Observe the figure below and find out their name.

Observe the figure below and find out their name.
Using the information given, name the right angles in part of figure:
AC ⊥ CD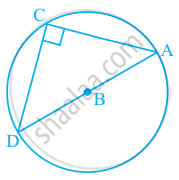
Using the information given, name the right angles in part of figure:
OP ⊥ AB