Advertisements
Advertisements
Question
Complete of the following, so as to make a true statement:
A point is in the interior of a convex quadrilateral, if it is in the ..... of its two opposite angles.
Solution
A point is in the interior of a convex quadrilateral, if it is in the interiors of its two opposite angles.
APPEARS IN
RELATED QUESTIONS
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
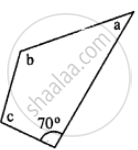
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
The diagonals of a rhombus are 6 .cm and 8 cm. State the angle at which these diagonals intersect.
Write two conditions that will make the adjoining figure a square.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is ______.
The number of right angles in a straight angle is ______ and that in a complete angle is ______.
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?