Advertisements
Advertisements
प्रश्न
Complete of the following, so as to make a true statement:
A point is in the interior of a convex quadrilateral, if it is in the ..... of its two opposite angles.
उत्तर
A point is in the interior of a convex quadrilateral, if it is in the interiors of its two opposite angles.
APPEARS IN
संबंधित प्रश्न
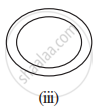
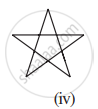
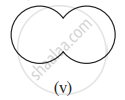
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
In a quadrilateral, define of the following Opposite angles .
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
Complete the following statement by means of one of those given in brackets against each:
If opposite angles of a quadrilateral are equal, then it is necessarily a ....................
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3 : 7 : 6 : 4, then ABCD is a ______.
A quadrilateral can be drawn when all the four angles and one side is given.
