Advertisements
Advertisements
प्रश्न
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.
उत्तर
Let exterior angle = x° & interior angle = 4x°
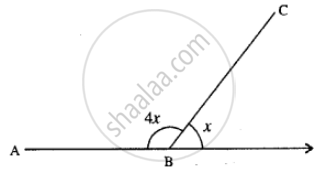
∴ 4x + x = 180°
5x = 180°
x = 36°
∴ Each exterior angle = 36°
Let no.of sides = n
∴ `360^circ/"n" = 36^circ`
n = `360^circ/36^circ`
n = 10
APPEARS IN
संबंधित प्रश्न
Fill in the blanks :
In case of regular polygon, with :
| No.of.sides | Each exterior angle | Each interior angle |
| (i) ___8___ | _______ | ______ |
| (ii) ___12____ | _______ | ______ |
| (iii) _________ | _____72°_____ | ______ |
| (iv) _________ | _____45°_____ | ______ |
| (v) _________ | __________ | _____150°_____ |
| (vi) ________ | __________ | ______140°____ |
Find the number of sides in a regular polygon, if its interior angle is: 160°
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Is it possible to have a regular polygon whose interior angle is: 135°
Is it possible to have a regular polygon whose interior angle is: 155°
Is it possible to have a regular polygon whose exterior angle is: 100°
Is it possible to have a regular polygon whose exterior angle is: 36°
