Advertisements
Advertisements
प्रश्न
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
उत्तर
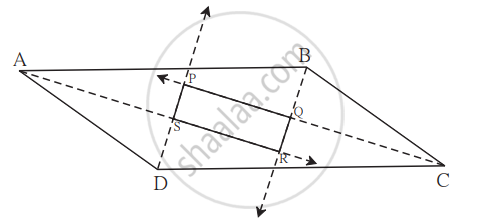
Given: `square`ABCD is a parallelogram.
To prove: `square`PQRS is a rectangle.
Proof:
`square`ABCD is a parallelogram. ...(Given)
∠ADC + ∠BCD = 180° ...(Adjacent angles of a parallelogram are supplementary.)
Multiplying each side by `1/2`,
`1/2` ∠ADC + `1/2` ∠BCD = `1/2xx180°` ...(i)
But,
`1/2` ∠ADC = ∠PDC ...(Ray DP bisects ∠ADC) ...(ii)
And `1/2` ∠BCD = ∠PCD ...(Ray CP bisects ∠BCD) ...(iii)
∴ ∠PDC + ∠PCD = 90° ...[From (i), (ii) and (iii)] ...(iv)
In ΔPDC,
∠PDC + ∠PCD + ∠DPC = 180° ...(The sum of the measures of the three angles of a triangle is 180°.)
∴ 90° + ∠DPC = 180° ...[from (iv)]
∴ ∠DPC = 180° – 90°
∴ ∠DPC = 90°
That means ∠SPQ = 90° ...(D-S-P, P-Q-C) ...(v)
Similarly, we can prove that, ∠SRQ = 90° ...(vi)
Similarly, ∠ASD = 90° and ∠BQC = 90° ...(vii)
∠PSR = ∠ASD ...(vertex angle)
∴ ∠PSR = 90° ...[From (vii)] ...(viii)
Similarly, ∠PQR = 90° ...(ix)
In `square`PQRS,
∠SPQ = ∠SRQ = ∠PSR = ∠PQR = 90° ...[From (v), (vi), (viii) and (ix)]
∴ `square`PQRS is a rectangle.
APPEARS IN
संबंधित प्रश्न
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Which of the following statement is true for a rectangle?
It has two pairs of equal sides.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
All rectangles are squares.
Which of the following statement is true for a square?
It is a rectangle.
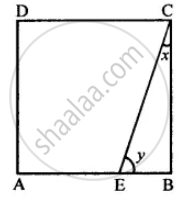
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Show that the bisectors of angles of a parallelogram form a rectangle
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
If diagonals of a quadrilateral are equal, it must be a rectangle.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
