Advertisements
Advertisements
प्रश्न
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
Advertisements
उत्तर
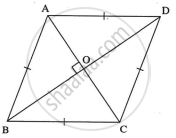
Let `square`ABCD be the rhombus.
AC = 20 cm, BD = 21 cm
AO = `1/2` AC ...[Diagonals of a rhombus bisect each other]
= `1/2 xx 20`
= 10 cm ...(i)
BO = `1/2` BD ...[Diagonals of a rhombus bisect each other]
= `1/2 xx21`
= `21/2`
= 10.5 cm ...(ii)
In ∆AOB,
∠AOB = 90° ...[Diagonals of a rhombus are perpendicular to each other]
By Pythagoras theorem,
∴ AB2 = AO2 + BO2
∴ AB2 = 102 + 10.52
∴ AB2 = 100 + 110.25
∴ AB2 = 210.25
∴ AB = `sqrt(210.25)`
∴ AB = 14.5 cm
Perimeter of `square`ABCD = 4 × AB
= 4 × 14.5
= 58 cm
APPEARS IN
संबंधित प्रश्न
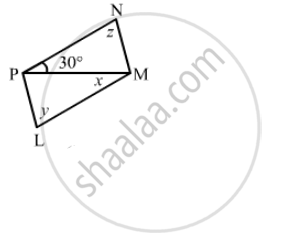
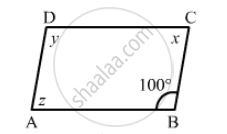
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
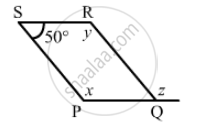
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
In the following figure GUNS and RUNS are parallelogram. Find x and y.
In the following figure GUNS and RUNS are parallelogram. Find x and y.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Find the angles marked with a question mark shown in Fig. 17.27
Which of the following statement is true for a rhombus?
It has two pairs of equal sides.
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
Which of the following statement is true for a rhombus?
It has all its sides of equal lengths.
Which of the following statement is true for a rhombus?
It can be a square.
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Show that each diagonal of a rhombus bisects the angle through which it passes.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
A quadrilateral whose all sides are equal, opposite angles are equal and the diagonals bisect each other at right angles is a ______.
