Advertisements
Advertisements
प्रश्न
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
उत्तर
Let ABCD be a rhombus where DE is perpendicular bisector of AB.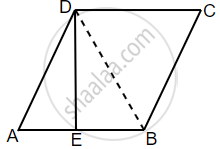
Construction: Join BD.
Now, in triangle AED and triangle BED:
AE = EB
ED = ED ...[Common side]
∠AED = ∠DEB = 90°
Now, using SAS rule,
ΔAED ≅ ΔBED
AD = DB = AB ...[ABCD is a rhombus. So, AD = AB]
Hence, triangle ADB is an equilateral triangle.
So, ∠DAB = ∠DBA = ∠ADB = 60°
∴ ∠DCB = 60° ...[Opposite angles of a rhombus are equal]
Now, ∠DAB + ∠ABC = 180° ...[Adjacent angles of a rhombus are supplementary]
⇒ 60° + ∠ABD + ∠DBC = 180°
⇒ 60° + 60° + ∠DBC = 180°
⇒ ∠DBC = 60°
⇒ ∠ABC = ∠ABD + ∠DBC = 60° + 60° = 120°
∴ ∠ADC = 120° ...[Opposite angles of a rhombus are equal]
Hence, the angles of the rhombus are 60°, 120°, 60°, 120°.
APPEARS IN
संबंधित प्रश्न
All rhombuses are parallelograms.
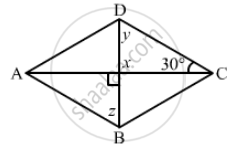
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
Which of the following statement is true for a rhombus?
It can be a square.
Fill in the blank, in each of the following, so as to make the statement true:
If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
Identify all the quadrilateral that have Four sides of equal length
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
