Advertisements
Advertisements
Question
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
Solution
Let ABCD be a rhombus where DE is perpendicular bisector of AB.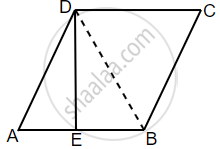
Construction: Join BD.
Now, in triangle AED and triangle BED:
AE = EB
ED = ED ...[Common side]
∠AED = ∠DEB = 90°
Now, using SAS rule,
ΔAED ≅ ΔBED
AD = DB = AB ...[ABCD is a rhombus. So, AD = AB]
Hence, triangle ADB is an equilateral triangle.
So, ∠DAB = ∠DBA = ∠ADB = 60°
∴ ∠DCB = 60° ...[Opposite angles of a rhombus are equal]
Now, ∠DAB + ∠ABC = 180° ...[Adjacent angles of a rhombus are supplementary]
⇒ 60° + ∠ABD + ∠DBC = 180°
⇒ 60° + 60° + ∠DBC = 180°
⇒ ∠DBC = 60°
⇒ ∠ABC = ∠ABD + ∠DBC = 60° + 60° = 120°
∴ ∠ADC = 120° ...[Opposite angles of a rhombus are equal]
Hence, the angles of the rhombus are 60°, 120°, 60°, 120°.
APPEARS IN
RELATED QUESTIONS
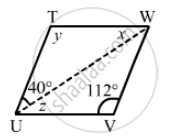
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
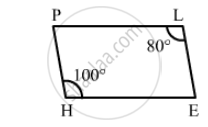
Can the following figure be parallelogram. Justify your answer.
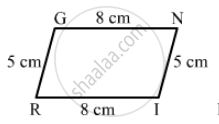
Can the following figure be parallelogram. Justify your answer.
Which of the following statement is true for a rhombus?
It has all its sides of equal lengths.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
Which of the following statement is true for a rectangle?
Its diagonals are equal and bisect each other.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

