Advertisements
Advertisements
Question
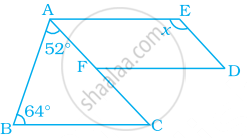
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
Solution
Let ABCD be a parallelogram, where BE and BF are the perpendiculars through the vertex B to the sides DC and AD, respectively.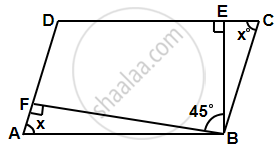
Let ∠A = ∠C = x, ∠B = ∠D = y ...[Opposite angles are equal in parallelogram]
Now, ∠A + ∠B = 180° ...[Adjacent sides of a parallelogram are supplementary]
In triangle ABF;
∠ABF = 90° – x
And in triangle BEC,
∠EBC = 90° – x
So, x + 90° – x + 45° + 90° – x = 180°
⇒ – x = 180° – 225°
⇒ x = 45°
So, ∠A = ∠C = 45°
∠B = 45° + 45° + 45° = 135°
⇒ ∠D = 135°
Hence, the angles are 45°, 135°, 45° and 135°.
APPEARS IN
RELATED QUESTIONS
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
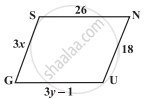
The following figure GUNS is a parallelogram. Find x and y. (Lengths are in cm)
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
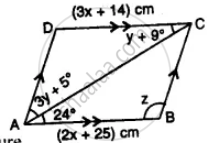
Use the information given in the alongside diagram to find the value of x, y, and z.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

All rectangles are parallelograms.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
In the following figure, FD || BC || AE and AC || ED. Find the value of x.