Advertisements
Advertisements
Question
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
Solution
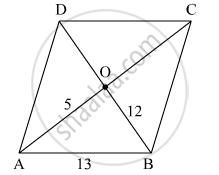
Given: AO = 5, BO = 12 and AB = 13
To Prove: `square`ABCD is a rhombus.
Proof:
AO2 + BO2
= 52 + 122
= 25 + 144
= 169 ...(i)
∴ AB2 = 132 = 169 ...(ii)
∴ AB2 = AO2 + BO2 ...[From (i) and (ii)]
∴ ∆AOB is a right-angled triangle. ...[Converse of Pythagoras theorem]
∴ ∠AOB = 90°
∴ seg AC ⊥ seg BD ...(iii) [A-O-C]
∴ In parallelogram ABCD,
∴ seg AC ⊥ seg BD ...[From (iii)]
∴ `square`ABCD is a rhombus. ...[A parallelogram is a rhombus perpendicular to each other]
APPEARS IN
RELATED QUESTIONS
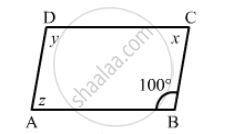
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
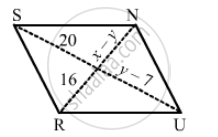
In the following figure GUNS and RUNS are parallelogram. Find x and y.
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
Fill in the blank, inthe following, so as to make the statement true:
A rhombus has all its sides of ...... length.
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is 'No', draw a figure to justify your answer.
In a rhombus PQRS if PQ = 7.5 cm then find QR. If ∠QPS = 75° then find the measure of ∠PQR and ∠SRQ.
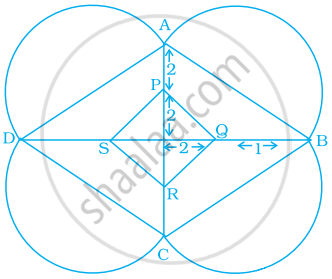
A Rangoli has been drawn on a flor of a house. ABCD and PQRS both are in the shape of a rhombus. Find the radius of semicircle drawn on each side of rhombus ABCD.