Advertisements
Advertisements
Question
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
Advertisements
Solution
\[\text{ Oppostie angles of a parallelogram are congurent } . \]
\[ \therefore \left( 3x - 2 \right)° = \left( 50 - x \right)°\]
\[3x°- 2° = 50°- x°\]
\[3x°+ x°= 50° + 2°\]
\[4x°= 52°\]
\[x° = 13°\]
\[\text{ Putting the value of x in one angle }: \]
\[3x° - 2°= 39°- 2°\]
\[ = 37°\]
\[\text{ Opposite angles are congurent }: \]
\[ \therefore 50 - x°\]
\[ = 37°\]
\[\text{ Let the remaining two angles be y and z } . \]
\[\text{ Angles y and z are congurent because they are also opposite angles } . \]
\[ \therefore y = z\]
\[\text{ The sum of adjacent angles of a paralle\logram is equal to } 180° . \]
\[ \therefore 37°+ y = 180°\]
\[y = 180°- 37°\]
\[y = 143°\]
\[\text{ So, the anlges measure are }: \]
\[37°, 37°, 143° \text{ and } 143°\]
RELATED QUESTIONS
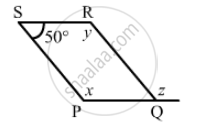
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
Can the following figure be parallelogram. Justify your answer.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
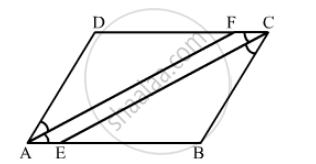
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
State with reason whether the following statement is ‘true’ or ‘false’.
Every rhombus is a rectangle.
If the diagonal of a rhombus are equal, then the rhombus is a
