Advertisements
Advertisements
Question
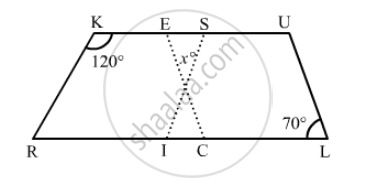
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
Solution
\[\text{ In the parallelogram RISK }: \]
\[\angle ISK + \angle RKS = 180° (\text{ sum of adjacent angles of a parallelogram is } 180°\]
\[\angle ISK = 180° - 120° = 60°\]
\[\text{ Similarly, in parallelogram CLUE }: \]
\[\angle CEU = \angle CLU = 70°(\text{ opposite angles of a parallelogram are equal })\]
\[\text{ In the triangle }: \]
\[x + \angle ISK + \angle CEU = 180°\]
\[x = 180° - \left( 70°+ 60° \right)\]
\[x = 180°- \left( 70°+ 60°\right) = 50°\]
APPEARS IN
RELATED QUESTIONS
All rhombuses are parallelograms.
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
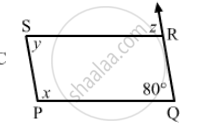
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
Which of the following statement is true for a rhombus?
It is a square.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Which of the following statement is true for a rectangle?
Its diagonals are equal and bisect each other.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
If the diagonal of a rhombus are equal, then the rhombus is a
A Rangoli has been drawn on a flor of a house. ABCD and PQRS both are in the shape of a rhombus. Find the radius of semicircle drawn on each side of rhombus ABCD.