Advertisements
Advertisements
Question
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
Advertisements
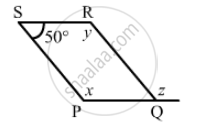
Solution
\[\text{ Opposite angles of a parallelogram are same } . \]
\[ \therefore x = y \text{ and } \angle RQP = 100°\]
\[\angle PSR + \angle SRQ = 180°\]
\[y + 50°= 180°\]
\[x = 180°- 50°\]
\[x = 130°\]
\[ \therefore x = 130°, y = 130° \]
\[ \text{ Since y and z are alternate angles, z }= 130° . \]
APPEARS IN
RELATED QUESTIONS
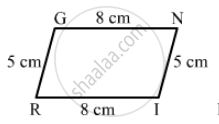
Can the following figure be parallelogram. Justify your answer.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
Draw a rhombus ABCD, if AB = 6 cm and AC = 5 cm.
Show that each diagonal of a rhombus bisects the angle through which it passes.
Which of the following statement is true for a rectangle?
Its diagonals are equal and bisect each other.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
If all sides of a quadrilateral are equal, it is a ______.
A rhombus is a parallelogram in which ______ sides are equal.
Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
