Advertisements
Advertisements
Question
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
Solution
No, it is not a rhombus. This is because diagonals of a rhombus must be perpendicular.
APPEARS IN
RELATED QUESTIONS
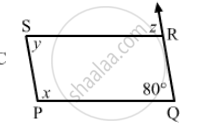
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
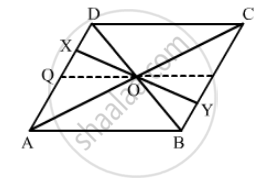
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
Which of the following statement is true for a rhombus?
It has two pairs of equal sides.
Which of the following statement is true for a rhombus?
It has all its sides of equal lengths.
Which of the following statement is true for a rhombus?
It is a square.
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is 'No', draw a figure to justify your answer.
Draw a rhombus ABCD, if AB = 6 cm and AC = 5 cm.
In rhombus ABCD;
(i) if ∠A = 74° ; find ∠B and ∠C.
(ii) if AD = 7.5 cm ; find BC and CD.
In a rhombus diagonals intersect at ______ angles.
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
