Advertisements
Advertisements
Question
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
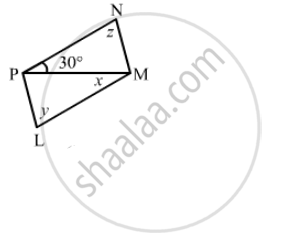
Solution
\[\text{ Sum of all angles in a triangle is } {180}^° . \]
\[ \therefore 30° + 90° + z = 180°\]
\[z = 60°\]
\[\text{ Opposite angles are equal in parallelogram } . \]
\[ \therefore y = z = 60°\]
\[\text{ and } x = 30° (\text{ alternate angles })\]
APPEARS IN
RELATED QUESTIONS
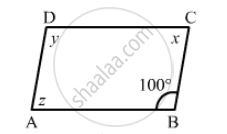
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
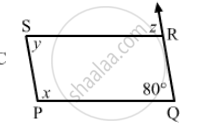
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
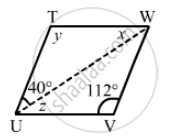
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
Which of the following statement is true for a rhombus?
It can be a square.
Fill in the blank, inthe following, so as to make the statement true:
A rhombus has all its sides of ...... length.
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
If a diagonal of a quadrilateral bisects both the angles, then it is a ______.
Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
