Advertisements
Advertisements
Question
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
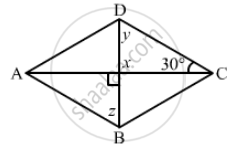
Solution
\[ x = 90° (\text{ vertically opposite angle })\]
\[\text{ Sum of all angles in a triangle is } {180}^°. \]
\[ \therefore y + 90°+ 30° = 180°\]
\[y = 180°- (90°+ 30°) = 60°\]
\[y = z = 60° (\text{ alternate angles })\]
APPEARS IN
RELATED QUESTIONS
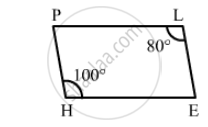
Can the following figure be parallelogram. Justify your answer.
Which of the following statement is true for a rhombus?
It is a square.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
If all pairs of adjacent sides of a quadrilateral are congruent then it is called ______.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
A rhombus is a parallelogram in which ______ sides are equal.
Construct a rhombus whose side is 5 cm and one angle is of 60°.
