Advertisements
Advertisements
Question
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
Solution
Given : Rhombus ABCD in which ∠BCA = 35°
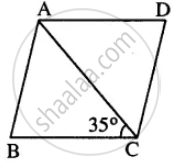
To find : ∠ADC
Proof : AD || BC
∠DAC = ∠BCA (Alternate ∠s)
But ∠BCA = 35° (Given)
∠DAC = 35°
But ∠DAC = ∠ACD ( AD = CD) & ∠DAC +∠ACD + ∠ADC = 180°
35°+ 35° + ∠ADC = 180°
∠ADC = 180° – 70° = 110°
Hence ∠ADC = 110°
APPEARS IN
RELATED QUESTIONS
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
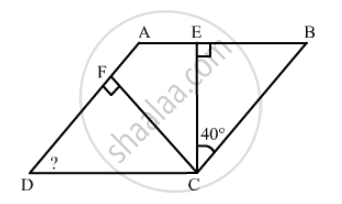
Find the angles marked with a question mark shown in Fig. 17.27
Which of the following statement is true for a rhombus?
It has two pairs of equal sides.
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
If the diagonal of a rhombus are equal, then the rhombus is a
A rhombus is a parallelogram in which ______ sides are equal.
