Advertisements
Advertisements
Question
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
Options
100°
80°
160°
40°
Solution
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is 40°.
Explanation:
A rhombus is also a parallelogram so, the opposite angles will be congruent.
Thus, (2x)° = (3x - 40)°
3x - 2x = 40°
x = 40°
APPEARS IN
RELATED QUESTIONS
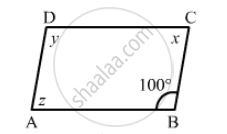
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
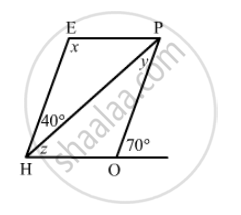
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
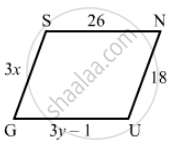
In the following figure GUNS and RUNS are parallelogram. Find x and y.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Which of the following statement is true for a rhombus?
It is a parallelogram.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
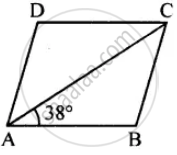
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
In a rhombus diagonals intersect at ______ angles.
