Advertisements
Advertisements
प्रश्न
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
पर्याय
100°
80°
160°
40°
उत्तर
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is 40°.
Explanation:
A rhombus is also a parallelogram so, the opposite angles will be congruent.
Thus, (2x)° = (3x - 40)°
3x - 2x = 40°
x = 40°
APPEARS IN
संबंधित प्रश्न
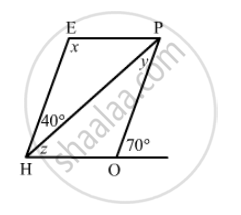
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
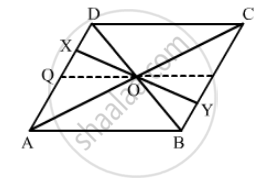
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
Which of the following statement is true for a rhombus?
It is a parallelogram.
Which of the following statement is true for a rhombus?
It can be a square.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
