Advertisements
Advertisements
प्रश्न
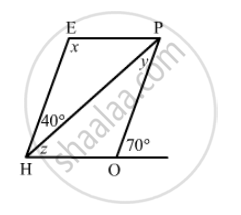
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
उत्तर
\[\angle HOP + 70°= 180° (\text{ linear pair })\]
\[\angle HOP = 180°- 70°= 110°\]
\[x = \angle HOP = 110° (\text{ opposite angles of a parallelogram are equal })\]
\[\angle EHP + \angle HEP = 180°(\text{ sum of adjacent angles of a parallelogram is } 180°)\]
\[110° + 40° + z = 180°\]
\[z = 180° - 150°= 30°\]
\[y = 40° \left( \text{ alternate angles }\right)\]
APPEARS IN
संबंधित प्रश्न
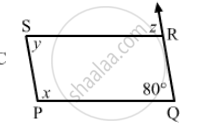
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
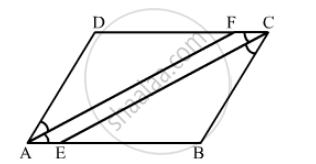
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
Fill in the blank, in each of the following, so as to make the statement true:
If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
Show that each diagonal of a rhombus bisects the angle through which it passes.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
