Advertisements
Advertisements
प्रश्न
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
उत्तर
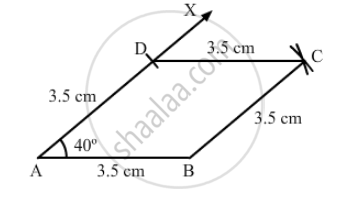
1. Draw a line segment AB of 3.5 cm.
2. Draw \[\angle\] BAX equal to 40\[°\]
3. With A as centre and the radius equal to AB, cut AD at 3.5 cm.
4. With D as centre, cut an arc of radius 3.5 cm.
5. With B as centre, cut an arc of radius 3.5 cm. This arc cuts the arc of step 4 at C.
6. Join DC and BC.
APPEARS IN
संबंधित प्रश्न
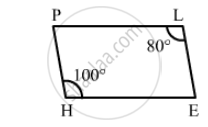
Can the following figure be parallelogram. Justify your answer.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E, AEand BC produced meet at F. Find te length CF.
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

A rhombus is a parallelogram in which ______ sides are equal.
