Advertisements
Advertisements
प्रश्न
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
उत्तर
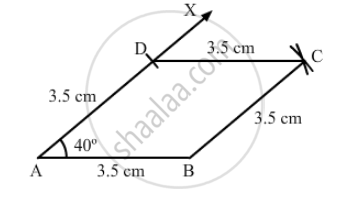
1. Draw a line segment AB of 3.5 cm.
2. Draw \[\angle\] BAX equal to 40\[°\]
3. With A as centre and the radius equal to AB, cut AD at 3.5 cm.
4. With D as centre, cut an arc of radius 3.5 cm.
5. With B as centre, cut an arc of radius 3.5 cm. This arc cuts the arc of step 4 at C.
6. Join DC and BC.
APPEARS IN
संबंधित प्रश्न
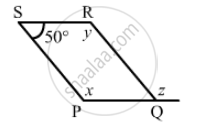
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
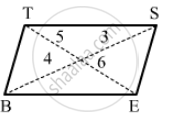
Can the following figure be parallelogram. Justify your answer.
Which of the following statement is true for a rhombus?
Two of its angles are at right angles
Which of the following statement is true for a rhombus?
It is a quadrilateral.
Fill in the blank, inthe following, so as to make the statement true:
A rhombus has all its sides of ...... length.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

