Advertisements
Advertisements
Question
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
Solution
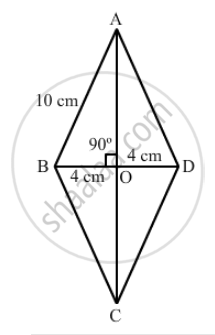
\[\text{ We know that the diagonals of a rhombus bisect each other at right angles }. \]
\[ \therefore BO = \frac{1}{2}BD = (\frac{1}{2} \times 16) cm\]
\[ = 8cm\]
\[AB = 10 \text{ cm and }\angle AOB = 90°\]
\[\text{ From right } ∆ OAB: \]
\[ {AB}^2 = {AO}^2 + {BO}^2 \]
\[ \Rightarrow {AO}^2 = ( {AB}^2 -{BO}^2 )\]
\[ \Rightarrow {AO}^2 = (10 )^2 - (8 )^2 {cm}^2 \]
\[ \Rightarrow {AO}^2 = (100 - 64) {cm}^2 = 36 {cm}^2 \]
\[ \Rightarrow AO = \sqrt{36} cm = 6cm\]
\[ \therefore AC = 2 \times AO = (2 \times 6) cm = 12 cm\]
APPEARS IN
RELATED QUESTIONS
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
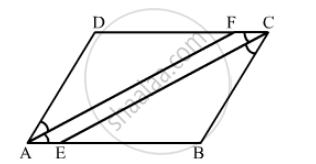
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
Fill in the blank, inthe following, so as to make the statement true:
A square is a rhombus in which .....
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
A quadrilateral whose all sides are equal, opposite angles are equal and the diagonals bisect each other at right angles is a ______.
A rhombus is a parallelogram in which ______ sides are equal.
