Advertisements
Advertisements
प्रश्न
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
उत्तर
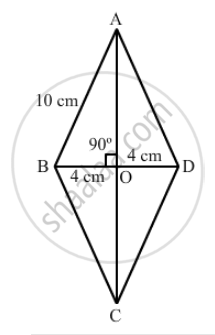
\[\text{ We know that the diagonals of a rhombus bisect each other at right angles }. \]
\[ \therefore BO = \frac{1}{2}BD = (\frac{1}{2} \times 16) cm\]
\[ = 8cm\]
\[AB = 10 \text{ cm and }\angle AOB = 90°\]
\[\text{ From right } ∆ OAB: \]
\[ {AB}^2 = {AO}^2 + {BO}^2 \]
\[ \Rightarrow {AO}^2 = ( {AB}^2 -{BO}^2 )\]
\[ \Rightarrow {AO}^2 = (10 )^2 - (8 )^2 {cm}^2 \]
\[ \Rightarrow {AO}^2 = (100 - 64) {cm}^2 = 36 {cm}^2 \]
\[ \Rightarrow AO = \sqrt{36} cm = 6cm\]
\[ \therefore AC = 2 \times AO = (2 \times 6) cm = 12 cm\]
APPEARS IN
संबंधित प्रश्न
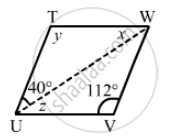
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
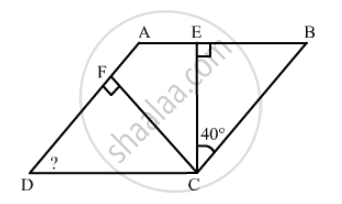
Find the angles marked with a question mark shown in Fig. 17.27
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
Which of the following statement is true for a rhombus?
Its diagonals are equal and perpendicular.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
