Advertisements
Advertisements
Question
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
Solution
\[\text{ Given that one angle of the parallelogram is } 70° . \]
\[\text{ Since opposite angles have same value, if one is }70° , \text{ then the one directly opposite will also be } 70° . \]
\[\text{ So, let one angle be }x° . \]
\[x° + 70° = 180° (\text{ the sum of adjacent angles of a parallelogram is } 180° )\]
\[x° = 180° - 70° \]
\[x° = 110° \]
\[\text{ Thus, the remaining angles are }110° , 110° \text{ and }70° . \]
APPEARS IN
RELATED QUESTIONS
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
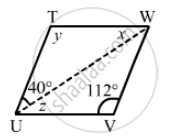
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
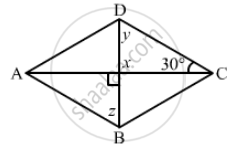
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
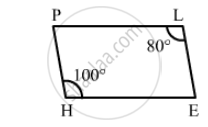
Can the following figure be parallelogram. Justify your answer.
Which of the following statement is true for a rhombus?
It can be a square.
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
Measure of one angle of a rhombus is 50°, find the measures of remaining three angles.
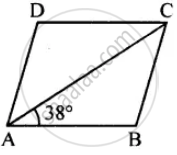
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.